Knobelaufgaben

Der Korb ist gefüllt – hier wurden viele Knobeleien mit Auflösungen eingestellt. Scrollt also herum und wählt euch aus, leicht und schwer, lustig und logisch …

Und hier gleich etwas zum Basteln, ein Spiel nach dem Muster von Monopoly, bei dem es um Zinsen, statt um Immobilien geht. Schaut mal rein!

Spielanleitung und Vordrucke für Geld hier S.  128 f

 

 

 

 

 

 

 

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Lösungen zu den Dezember-Knobeleien

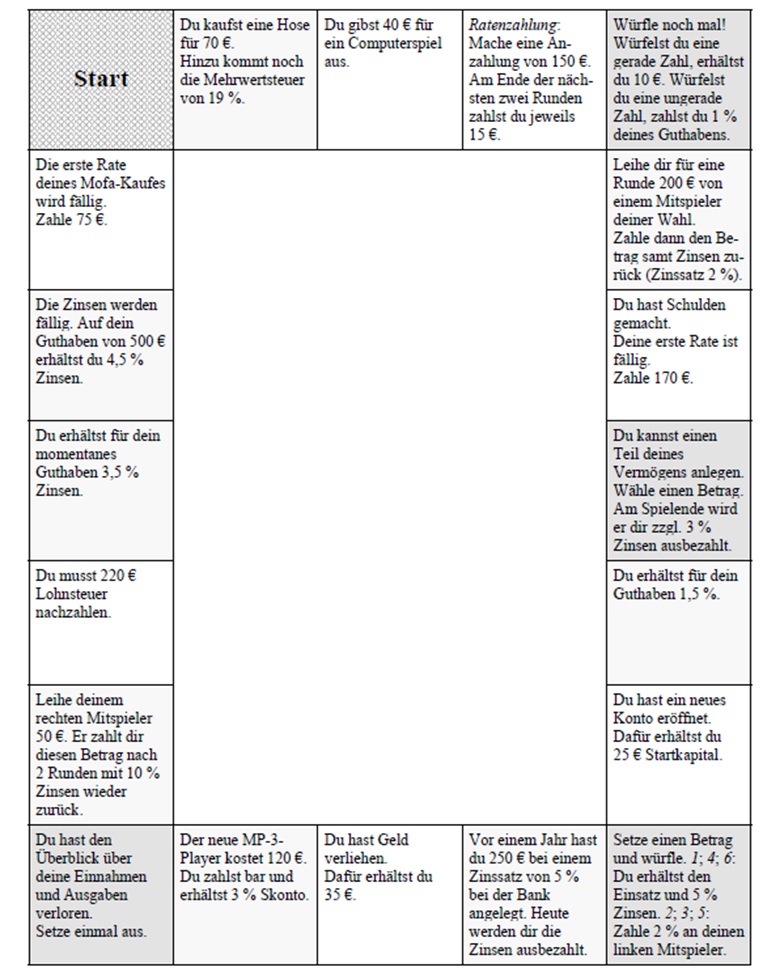
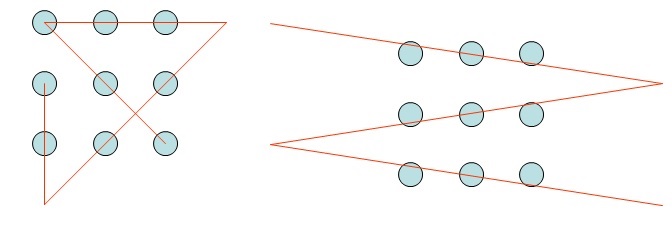
Zum 9-Punkte-Problem

 

Zum Suchspiel

 

 

 

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Dezember   Als Erstes ein Suchspiel      

Und dann ein „klassisches“ Problem – viel Spaß!

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Lösungen zu den letzten Aufgaben:

 Fasane, Hasen und Rehe   

Wer hat den Ball geworfen?  

 

 

 

Distanz Löwe – Bär         Klicken, um zu vergrößern

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Die letzten Aufgaben waren:                               

1.   Zum Wiedereingewöhnen eine ‚einfache‘ Frage:   Fasane, Hasen und Rehe   

Ein Fasan kostet 0,50 Franken, ein Hase 3 Franken und ein Reh 7 Franken.
Wie viele Tiere sind von jeder Tiersorte zu nehmen, wenn 100 Tiere 100 Franken kosten und von jeder Sorte mindestens ein Tier zu nehmen ist?

2.  Wer von euch vier hat den Ball in mein Fenster geworfen?

Wenn nur einer der vier gelogen hat, wer hat dann den Ball geworfen?
Wenn nur einer die Wahrheit gesagt hat, wer war dann der Täter?

3. Für tüchtige Mathematiker:   Wie weit ist es vom „Löwen“ zum „Bären“

(Die Aufgabe ist nicht ganz einfach. Sie führt auf ein Gleichungssystem von 4 Gleichungen mit 4 Unbekannten!)

Nach einem Becher im „Löwen“ macht sich Herr Bieri (mit konstanter Geschwindigkeit) auf den Weg zum „Bären“. Zur gleichen Zeit bricht Herr Weinhold vom „Bären“ in Richtung „Löwen“ auf.  Bis zum Treffpunkt legt Herr Bieri 200 Meter mehr als Herr Weinhold zurück. Nach einem Gespräch gehen sie weiter, wegen Nachsinnen über das zufällige Treffen aber jeweils nur noch mit halber Geschwindigkeit. Herr Bieri benötigt noch 8 Minuten bis zum „Bären“, Herr Weinhold noch 18 Minuten bis zum „Löwen“. Berechne die Entfernung vom „Löwen“ zum „Bären“.

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Lösungen für Oktober/November  

Drei Fragen zum Überleben

 Lösung von Robert Israel    http://www.janko.at/Raetsel/Logik/025.b.htm

Frage 1: Ist es wahr, dass entweder Tür 1 in die Freiheit führt oder die Antwort auf diese Frage eine Lüge ist?

Frage 2: Ist es wahr, dass entweder Tür 2 in die Freiheit führt oder die Antwort auf diese Frage eine Lüge ist?

Frage 3: Ist es wahr, dass entweder Tür 3 in die Freiheit führt oder die Antwort auf diese Frage eine Lüge ist?

Lösung von Kevin Wald       http://www.janko.at/Raetsel/Logik/025.b.htm

Frage 1: Ist zwei plus zwei gleich vier?

Wenn die Antwort „ja“ lautet, können wir direkt nach zwei der Türen fragen. Die Antworten werden Lügen sein. Wenn die Antwort „nein“ lautet, wird die Antwort auf die Fragen 2 und 3 einmal wahr und einmal falsch sein und wir stellen unsere zweite Frage:

Frage 2: Würde meine dritte Frage „Führt Türe 1 in die Freiheit“ mit „ja“ beantwortet werden?

Wird diese Frage wahrheitsgemäß beantwortet, muss Frage 3 falsch beantwortet werden und umgekehrt. Wie auch immer, die Antwort auf Frage 2 muss „nein“ lauten, wenn die Türe 1 in die Freiheit führt.

Falls der Aufseher mit „ja“ antwortet, stellen wir eine dritte Frage:

Frage 3: Würde meine Frage „Führt Türe 2 in die Freiheit“ mit „ja“ beantwortet werden?

Der Gefangene und die Türen

Die Zugfolge CBCACBC führt immer zum Ziel.

Fall 1: 2 Riegel sind auf der einen Seite, 2 auf der anderen.

Fall 1a: R1 und R3 sind auf derselben Seite. Dann sind wir nach einmaligem Drücken von C befreit.

Fall 1b: Die Riegel, die auf derselben Seite sind, sind zyklisch benachbart. („Zyklisch“ soll heißen, dass R1 und R4 auch benachbart sind.) Nach C ist das immer noch so. B ergibt nun entweder schon die Befreiungsstellung oder die unter 1a beschriebene Situation; spätestens nach dem nächsten C sind wir dann frei.

Fall 2: 3 Riegel sind auf der einen Seite, 1 auf der anderen. Nach CBC ist das immer noch so (da B, C paritätserhaltend sind). A bringt uns entweder zur Befreiung oder in Fall 1. Dort sind wir spätestens nach weiterem CBC befreit.

 Porcias Kästchen  

 Mindestens 3 Inschriften sind falsch – Lösung für Originalaufgabe

Das Bild ist in Kästchen 3.

 

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Aufgaben für Oktober/November

 Hier drei Aufgaben, die mit logischem Denken zu lösen sind – ziemlich knifflich, nicht wahr? (Quelle: http://www.janko.at/Raetsel/)

 1.   Drei Fragen zum Überleben

Sie befinden sich in einem großen Raum, dessen drei Ausgänge von einem Aufseher bewacht werden. Sie wissen nicht, wie und warum Sie hier sind, aber das ist letztlich auch egal. Allerdings erinnern Sie sich daran, dass Sie heute Abend ein Rendezvous mit Ihrer Freundin haben, das Sie keinesfalls verpassen möchten.  –  Sie sprechen den Aufseher an, und dieser antwortet: „Eine der drei Türen führt in die Freiheit, die anderen beiden in den Tod. Du darfst mit drei fragen stellen, die ich mit ‚ja‘ oder ’nein‘ beantworten werde. Aber sei gewarnt, ich werde genau ein mal die Wahrheit sagen und die beiden anderen male lügen.“   –   Welche Fragen müssen Sie stellen, um die Verabredung mit Ihrer Freundin einhalten zu können?

 2. Der Gefangene und die Türen

3.     Porcias Kästchen

Porcia, die reiche junge Adelige aus Shakespeares Der Kaufmann von Venedig hat vier Kästchen; in einem von ihnen ist Porcias Bild verborgen. An jedem Kästchen ist ein Schild angebracht, dessen Inschrift entweder wahr oder falsch ist. Ein Freier musste herausfinden, in welchem Kästchen Porcias Bild war. Gelang ihm dies, durfte er Porcia ehelichen; anderenfalls musste er zeitlebens ehelos bleiben.

Mindestens 3 Inschriften sind falsch.

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Lösungen für Juli/August

Wie hoch ist der Gewinn? – Ich komme auf 2 Mark. Lest aber einmal diese Diskussion, die noch auf weitere – teils witzige – Überlegungen geht:

http://www.dasgelbeforum.net/ewf2000/board_entry.php?id=243010&page=83&order=name&category=0

Zahlensalat – Die gesuchte Zahl lautet 23421314 oder rückwärts 41312432.

Der Bettler und der Bauer –

2, 2 und 9 Jahre sind die richtige Antwort. Woher der Bettler die Hausnummer weiß bleibt ein Geheimnis. Es gibt jedoch zwei Kombinationen, bei denen das Produkt 36 ist und deren Summe gleich ist (1, 6, 6 = 13 und 2, 2, 9 = 13). Aus diesem Grund hat die Hausnummer allein auch nicht weitergeholfen. Erst der Hinweis, dass es einen ältesten Sohn gibt, führt zur Lösung.

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Aufgaben für  Juli/August

Wie hoch ist der Gewinn?

Ein Händler kaufte eine Ware für sieben Mark, verkaufte sie für acht Mark, kaufte sie für neun Mark zurück und verkaufte sie wieder für zehn Mark. Wieviel hat er dabei verdient?

Zahlensalat

Gesucht wird eine achtstellige Zahl, die 2 Einsen, 2 Zweien, 2 Dreien und 2 Vieren enthält. Die Einsen in dieser Zahl sind durch eine Zahl voneinander getrennt, die Zweien durch zwei Stellen, die Dreien durch drei und die Vieren durch vier Stellen.  Wie lautet die Zahl?

Der Bettler und der Bauer (Achtung! Logisch, aber um die Ecke herum)

Ein Bettler möchte von einem Bauer wissen, wie alt seine Söhne sind. Zwischen Beiden spielt sich folgender Dialog ab:
Bettler: „Wie alt sind denn ihre drei Söhne?“
Bauer: „Wenn man ihr Alter miteinander multipliziert, dann kommt 36 heraus. Wenn man ihr Alter addiert, ergibt dies unsere Hausnummer.“
Bettler: „Jetzt kenne ich ihre Hausnummer, aber …“
Bauer: „Hören Sie doch nur, wie gut unser Ältester Geige spielt!“
Bettler: „Vielen Dank für die Auskunft – jetzt weiß ich die Lösung.“
Wie alt sind nun die Söhne des Bauers?

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Lösungen für Juni

Felder verbinden

Farbige Marken

Nur von C kann man die Farbe bestimmen. Wenn C’s Marke rot gewesen wäre, dann hätte B durch folgende Überlegung gewusst, dass seine Marke nicht rot war:

„Wenn meine Marke auch rot wäre, dann würde A zwei rote Marken sehen und wissen, dass seine Marke nicht rot ist. Aber A weiß nicht, daß seine Marke nicht rot ist. Darum kann meine Marke nicht rot sein.“

Daraus folgt, dass, wenn C’s Marke rot gewesen wäre, B gewusst hätte, dass seine Marke nicht rot ist. Aber B wusste nicht, dass seine Marke nicht rot war, darum konnte C’s Marke nicht rot gewesen sein.

Wenn man das Wort „rot“ durch „gelb“ ersetzt, zeigt dieselbe Argumentation, dass C’s Marke auch nicht gelb war. Darum muss C’s Marke grün sein.

Der Bär

Der Mann wohnt genau auf dem Nordpol. Wenn er 1 Km in südlicher Richtung geht ist er logischerweise genau 1 Km von seinem Haus entfernt. Nun kann er beliebig weit in westlicher oder östlicher Richtung gehen ohne sich weiter von seinen Haus zu entfernen als 1 Km. Sobald er dann wieder nach Norden geht läuft er immer in die Richtung seines Hauses. Der Bär ist also ein Eisbär und Weiss.

Politiker

Vorausgesetzt wird, dass zumindestens eine Person unbestechlich ist. Nimmt man irgendeine unbestechliche Person heraus. Jetzt nimmt man eine der verbleibenen 99 Personen. Gemäß der zweiten Vereinbarung ist diese bestechlich. Da die zweite Person für jede andere der 99 Personen steht, so muss jeder der übrigen bestechlich sein. Die Antwort lautet somit das einer der Politiker unbestechlich und 99 Politiker bestechlich sind.

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Aufgaben für Juni

Felder verbinden

 Farbige Marken

Drei Personen – A, B und C – waren allesamt perpekte Logiker. Jeder konnte sofort sämtliche Folgerungen aus jeder Menge von Voraussetzungen ableiten. Jeder war sich auch im Klaren, dass jeder der beiden Anderen logisches Denken perfekt beherrschte. Man zeigte den Dreien sieben Marken: zwei rote, zwei gelbe und drei grüne. Dann band man ihnen die Augen zu und klebte jedem eine Marke auf die Stirn. Die restlichen Marken kamen in eine Schublade. Nachdem die Augenbinden abgenommen worden waren, fragte man A: „Kennen Sie eine Farbe, die Sie bestimmt nicht haben?“ „Nein“, antwortete A. – Dann stellte man B dieselbe Frage, und er sagte: „Nein“.

Ist es möglich, von diesen Informationen auf die Farbe der Marke zu schließen, die A, B und C auf der Stirn trugen?

 Der Bär

Ein Mann kommt aus seiner Haustür und geht etwa einen Kilometer in genau südlicher Richtung. Danach geht er 4 km nach Westen. Dort begegnet er auf einmal einem Bären. Der Mann rennt wie wild um sein Leben, und zwar genau einen Kilometer weit nach Norden. Dort stößt er dann genau wieder auf sein Haus. Welche Farbe hat der Bär?

 

Politiker

In einer nicht näher bestimmten politischen Versammlung debattierten einhundert Politiker miteinander. Jeder von ihnen war entweder bestechlich oder unbestechlich. Folgende Tatsachen sind uns bekannt:

a             Zumindest einer der Politiker war unbestechlich.

b             Von jeweils zwei Politikern war wenigstens einer bestechlich.

Kann aus diesen zwei Tatsachen geschlossen werden, wie viele der Politiker bestechlich und wie viele unbestechlich waren?

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

 Lösung für April

  Zum Flaschenproblem:

 

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Die neuen Aufgaben für April – Viel Spaß!

Flaschenproblem:     Gegeben sind drei Flaschen, deren Fassungsvermögen exakt acht, fünf und drei Liter beträgt. Die acht-Liter-Flasche sei randvoll gefüllt, die anderen leer. Man fülle nun so um, daß sich in zwei Gefäßen jeweils vier Liter befinden.

Wie hoch ist das Haus?   Und hier eine Geschichte, die man nur nachmachen sollte, wenn man sicher ist, dass man ähnlich viel drauf hat, wie der Held dieser Geschichte.

Zu Nils Bohr: http://www.wasistwas.de/archiv-wissenschaft-details/dem-atom-auf-der-spur-niels-bohr.html

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Lösungen für Februar:

In memoriam: Nein – zumindest wurde er nicht 1933 aufgestellt, denn die Einteilung in Ersten und Zweiten Weltkrieg fand erst nach dem Zweiten Weltkrieg statt.

Münzen Aufgabe                 

 

Streichholz Aufgabe:                         

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Aufgaben im Februar:

In memoriam     „In treuem Gedenken an die Männer, die im Ersten Weltkrieg ihr Leben für uns geopfert haben.“ Mit dieser Inschrift wurde im August 1933 der Gefallenen des Ortes Marsweiler gedacht. Das zumindest behauptet die örtlichen Chronik, denn der Gedenkstein gilt als verschollen. Hat es ihn je gegeben?

Münzen Aufgabe    Du hast 10 Münzen. Du sollst sie so anordnen, dass sie 5 Gerade bilden, auf denen je 4 Münzen liegen.

Streichholz Aufgabe    Du hast 6 Streichhölzer. Du sollst sie so anordnen, dass sie 4 gleichseitige Dreiecke bilden. Die Hölzer dürfen sich nicht kreuzen und du darfst sie selbstverständlich nicht brechen.

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Bevor wir die Lösungen für Januar geben, hier eine Anfrage von D. zu den Lösungen der Zahlenreihe (September):

D. fragt: Wie kommt denn beim ersten Zug die 1 an die letzte Stelle bzw. eine 21 statt eine 12? Hier eine Übersicht des ersten Zuges:                                                                                                                                                            

 

 

Als wir das überprüft haben, hat uns der Bindestrich  bei den Lösungen irritiert. Er führt auf unzutreffende Annahmen, nämlich, dass nur die 1 bewegt worden sei. Das ist aber nach der Regel nicht möglich. Die Bedeutung des Bindestrichs können wir nicht nachvollziehen. Denkt ihn euch fort!

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Lösungen für Januar

Wasserlilienproblem

Wenn die Lilien ihre Ausdehnung auf der Oberfläche täglich verdoppeln, wird der See nach 59 Tagen zur Hälfte bedeckt sein.
Bis zum 60. Tag verdoppeln die Lilien ein letztes Mal ihre Ausdehnung auf der Oberfläche, und der See ist vollkommen bedeckt.

Indianerrätsel

Zuerst gehen 5 und 10, 10 bleibt drueben, 5 geht zurueck (mit Lampe), 15 min gesamt vergangen.Dann gehen 20 und 25 rueber, 10 geht zurueck (mit Lampe), 50 min vergangen.Schliesslich geht 5 mit 10 rueber und wir sind bei 60 min Gesamtzeit – logisch, oder!?

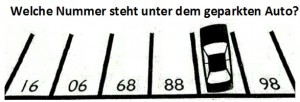
Parkplatz Problem

Antwort : 87    Mache dir klar, wie das Auto geparkt ist.  Man schaut  von der Rückseite des Parkplatzes auf die Autos. Drehe das Bild um 180 Grad. Jetzt ist dir die Lösung klar.

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Knobelaufgaben für Januar 2016

Das Wasserlilienproblem

Auf einem bestimmten See verdoppeln Wasserlilien alle 24 Stunden ihre Ausdehnung auf der Oberfläche. Vom Tag an, da die erste Wasserlilie erscheint, bis der See vollkommen bedeckt ist, dauert es 60 Tage.  –   An welchem Tag ist der See zur Hälfte bedeckt?

Das Indianerrätsel

Vier verletzte Indianer müssen eine Hängebrücke passieren. Die vier brauchen je 5, 10, 20 und 25 Minuten, um die Brücke zu überqueren (von einer Seite auf die andere). Da es schon dunkel ist, müssen sie bei jeder Überquerung die eine Lampe, die an der Brücke steht, mitnehmen. Die Brücke ist schon so morsch, daß sie nur zwei Indianer gleichzeitig trägt. Das heißt: es gehen immer zwei rüber, dann muss wieder einer mit der Lampe zurück. Finden Sie einen Weg, so daß alle vier (und die Lampe) nach 60 Minuten drüben sind.

Das Parkplatz-Problem

 

 

 

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Und hier die Lösungen für die Septemberaufgaben!

Lösung Zahlenreihe

 Lösung Anja und Maik

Lösung „Wer darf am Apfel naschen“ – na, das habt ihr sicher allein herausgefunden!

♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦♦

Knobelaufgaben im September